no free lunch

i’m always looking for a free lunch.

a free ticket, a free pass, a free solution to all the problems i’ve been avoiding and goals i’m trying to hit.

this week, dr. leslie hit me with the facts – there’s no such thing as a free lunch.

when modelling the real world, it’s easy to behave that we are all in the pursuit of the ultimate model that solves the whole thing. it turns out this is not true.

the no free lunch theorem states that any improvement in modelling functions over one class of problems will result in the offset of accuracy over another set of problems. on top of this, summing all these offset when we consider each how each model performs over all the problem spaces, they will all end up performing randomly badly. if we look at each model over an increasingly large number of problem spaces, this randomness will converge to equally bad average performance.

we can’t say how “good” a model is when looking at all problem spaces without just trying each one out and seeing how it does – there is no intristic characterisitc of a model that make it generally better than another.

as long as the entire solution space of the universe is split into 2 or more groups, even if we have an optimum model for one, it will always be suboptimal on the remaining space, and will even out across problem spaces to equal performance with other models.

you might be thinking – who cares?

humans will plausibly never be able to consider the entire problem space at once, for every possible problem that can exist. we will always be limited to some small subset of both problem spaces and models, both out of practical limtiations and the fact we just don’t care about a lot of problem spaces.

i think i probably don’t care either, overall. but knowing that a great way of modelling the world is definitely going to be trash along another set of problems to solve, feels important to know, and i don’t think is super obvious.

---

unfinished notes:

i learnt the free lunch theorem in the context of learning the perceptron algorithm

the perceptron algorithm is a linear classification algorithm that helps you move closer, in a seesaw motion to an optimum linear classifier, asumming one exists. you will definitely get there with this algorithm, and the max number of steps you both need is both definable and not that big.

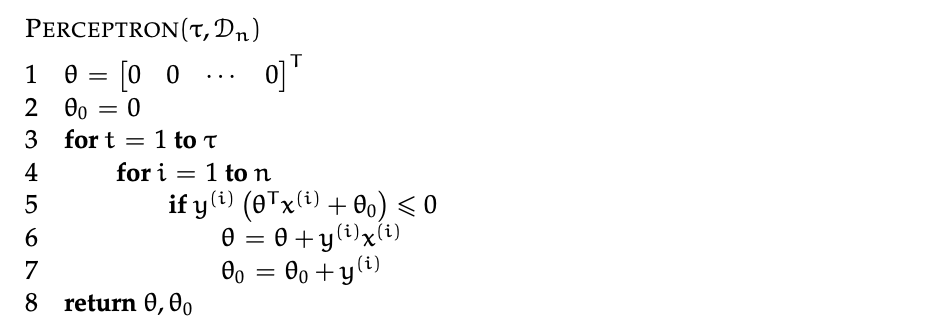
intuitively, if the an iteration of the algorithm “fails” (returns true on line 5), then the main defining parameter of the model, θ, moves 𝑥 closer to in direction 𝑦